Assignment #3-1의 Fully Connected Network에 이어서
이제는 Convolutional Neural Network와 Batch Noramlization을 다룬다.
class Conv(object):
@staticmethod
def forward(x, w, b, conv_param):
"""
A naive implementation of the forward pass for a convolutional layer.
The input consists of N data points, each with C channels, height H and
width W. We convolve each input with F different filters, where each filter
spans all C channels and has height HH and width WW.
Input:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- 'stride': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- 'pad': The number of pixels that will be used to zero-pad the input.
During padding, 'pad' zeros should be placed symmetrically (i.e equally on both sides)
along the height and width axes of the input. Be careful not to modfiy the original
input x directly.
Returns a tuple of:
- out: Output data, of shape (N, F, H', W') where H' and W' are given by
H' = 1 + (H + 2 * pad - HH) / stride
W' = 1 + (W + 2 * pad - WW) / stride
- cache: (x, w, b, conv_param)
"""
out = None
##############################################################################
# TODO: Implement the convolutional forward pass. #
# Hint: you can use the function torch.nn.functional.pad for padding. #
# Note that you are NOT allowed to use anything in torch.nn in other places. #
##############################################################################
# Replace "pass" statement with your code
stride = conv_param['stride']
pad = conv_param['pad']
N, C, H, W = x.shape
F, C, HH, WW = w.shape
Hout = 1 + (H + 2 * pad - HH) // stride
Wout = 1 + (W + 2 * pad - WW) // stride
x = torch.nn.functional.pad(x, (pad, pad, pad, pad))
out = torch.zeros((N, F, Hout, Wout), dtype = x.dtype, device = x.device)
for n in range(N):
for f in range(F):
for i in range(Hout):
for j in range(Wout):
out[n,f,i,j] = (x[n,:, i * stride : i * stride + HH, j * stride : j * stride + WW] * w[f]).sum() + b[f]
#############################################################################
# END OF YOUR CODE #
#############################################################################
cache = (x, w, b, conv_param)
return out, cache
@staticmethod
def backward(dout, cache):
"""
A naive implementation of the backward pass for a convolutional layer.
Inputs:
- dout: Upstream derivatives.
- cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
Returns a tuple of:
- dx: Gradient with respect to x
- dw: Gradient with respect to w
- db: Gradient with respect to b
"""
dx, dw, db = None, None, None
#############################################################################
# TODO: Implement the convolutional backward pass. #
#############################################################################
# Replace "pass" statement with your code
x, w, b, conv_param = cache
dx = torch.zeros_like(x)
dw = torch.zeros_like(w)
db = torch.zeros_like(b)
N, F, Hout, Wout = dout.shape
F, C, HH, WW = w.shape
pad = conv_param['pad']
stride = conv_param['stride']
for n in range(N):
for f in range(F):
for i in range(Hout):
for j in range(Wout):
dx[n, :, i * stride: i * stride + HH, j * stride : j * stride + WW] += w[f] * dout[n,f,i,j]
dw[f] += dout[n,f,i,j] * x[n, :, i * stride: i * stride + HH, j * stride : j * stride + WW]
db[f] += dout[n,f,i,j]
dx = dx[:,:,pad:-1 * pad,pad:-1 * pad]
#############################################################################
# END OF YOUR CODE #
#############################################################################
return dx, dw, db
먼저 Conv 레이어의 forward와 backward부터 구현하는데 out = Wx + b라는 공식과
각 필터가 x의 데이터 공간 상을 stride만큼 이동하며 적용된다는 사실에 유의하며 구현하면 된다.
class MaxPool(object):
@staticmethod
def forward(x, pool_param):
"""
A naive implementation of the forward pass for a max-pooling layer.
Inputs:
- x: Input data, of shape (N, C, H, W)
- pool_param: dictionary with the following keys:
- 'pool_height': The height of each pooling region
- 'pool_width': The width of each pooling region
- 'stride': The distance between adjacent pooling regions
No padding is necessary here.
Returns a tuple of:
- out: Output data, of shape (N, C, H', W') where H' and W' are given by
H' = 1 + (H - pool_height) / stride
W' = 1 + (W - pool_width) / stride
- cache: (x, pool_param)
"""
out = None
#############################################################################
# TODO: Implement the max-pooling forward pass #
#############################################################################
# Replace "pass" statement with your code
pH = pool_param['pool_height']
pW = pool_param['pool_width']
stride = pool_param['stride']
N, C, H, W = x.shape
Hout = 1 + (H - pH) // stride
Wout = 1 + (W - pW) // stride
out = torch.zeros((N, C, Hout, Wout), dtype = x.dtype, device = x.device)
for n in range(N):
for i in range(Hout):
for j in range(Wout):
out[n, :, i, j], _ = x[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW].reshape(C, -1).max(axis = 1)
#############################################################################
# END OF YOUR CODE #
#############################################################################
cache = (x, pool_param)
return out, cache
@staticmethod
def backward(dout, cache):
"""
A naive implementation of the backward pass for a max-pooling layer.
Inputs:
- dout: Upstream derivatives
- cache: A tuple of (x, pool_param) as in the forward pass.
Returns:
- dx: Gradient with respect to x
"""
dx = None
#############################################################################
# TODO: Implement the max-pooling backward pass #
#############################################################################
# Replace "pass" statement with your code
x, pool_param = cache
pH = pool_param['pool_height']
pW = pool_param['pool_width']
stride = pool_param['stride']
N, C, H, W = x.shape
Hout = 1 + (H - pH) // stride
Wout = 1 + (W - pW) // stride
dx = torch.zeros_like(x)
for n in range(N):
for i in range(Hout):
for j in range(Wout):
local = x[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW]
local_shape = local.shape
local = local.reshape(C, -1)
local_dx = torch.zeros_like(local)
_, idx = local.max(axis = 1)
local_dx[range(C), idx] = dout[n, :, i, j]
dx[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW] = local_dx.reshape(local_shape)
#############################################################################
# END OF YOUR CODE #
#############################################################################
return dxclass MaxPool(object):
@staticmethod
def forward(x, pool_param):
"""
A naive implementation of the forward pass for a max-pooling layer.
Inputs:
- x: Input data, of shape (N, C, H, W)
- pool_param: dictionary with the following keys:
- 'pool_height': The height of each pooling region
- 'pool_width': The width of each pooling region
- 'stride': The distance between adjacent pooling regions
No padding is necessary here.
Returns a tuple of:
- out: Output data, of shape (N, C, H', W') where H' and W' are given by
H' = 1 + (H - pool_height) / stride
W' = 1 + (W - pool_width) / stride
- cache: (x, pool_param)
"""
out = None
#############################################################################
# TODO: Implement the max-pooling forward pass #
#############################################################################
# Replace "pass" statement with your code
pH = pool_param['pool_height']
pW = pool_param['pool_width']
stride = pool_param['stride']
N, C, H, W = x.shape
Hout = 1 + (H - pH) // stride
Wout = 1 + (W - pW) // stride
out = torch.zeros((N, C, Hout, Wout), dtype = x.dtype, device = x.device)
for n in range(N):
for i in range(Hout):
for j in range(Wout):
out[n, :, i, j], _ = x[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW].reshape(C, -1).max(axis = 1)
#############################################################################
# END OF YOUR CODE #
#############################################################################
cache = (x, pool_param)
return out, cache
@staticmethod
def backward(dout, cache):
"""
A naive implementation of the backward pass for a max-pooling layer.
Inputs:
- dout: Upstream derivatives
- cache: A tuple of (x, pool_param) as in the forward pass.
Returns:
- dx: Gradient with respect to x
"""
dx = None
#############################################################################
# TODO: Implement the max-pooling backward pass #
#############################################################################
# Replace "pass" statement with your code
x, pool_param = cache
pH = pool_param['pool_height']
pW = pool_param['pool_width']
stride = pool_param['stride']
N, C, H, W = x.shape
Hout = 1 + (H - pH) // stride
Wout = 1 + (W - pW) // stride
dx = torch.zeros_like(x)
for n in range(N):
for i in range(Hout):
for j in range(Wout):
local = x[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW]
local_shape = local.shape
local = local.reshape(C, -1)
local_dx = torch.zeros_like(local)
_, idx = local.max(axis = 1)
local_dx[range(C), idx] = dout[n, :, i, j]
dx[n, :, i * stride : i * stride + pH, j * stride : j * stride + pW] = local_dx.reshape(local_shape)
#############################################################################
# END OF YOUR CODE #
#############################################################################
return dx이어서 Max-pooling 레이어의 forward와 backward를 구현하면 되는데, forward는 Conv Layer의 forward에서
했던 것처럼 pooling이 적용되는 영역을 순회하면서 max값만 뽑아내면 되어서 쉽게 할 수 있을 것이다.
문제는 backward인데, pooling을 적용받은 영역에서 max인 경우에는 upstream gradient에서 값을 받아오고,
max가 아니면 0을 가져야 한다. 이전의 ReLU 레이어에서는 데이터의 차원이 그대로 유지되어 간단히 할 수 있었지만,
pooling 레이어는 그렇지 않아서 forward에서 했던 것처럼 pooling이 적용되는 영역을 순회하면서 해당 영역에서 max값을 갖는 위치를 찾아준다. 그리고 그 위치에 upstream gradient를 넣어주고 나머지는 0으로 만들어주면 된다.
class ThreeLayerConvNet(object):
"""
A three-layer convolutional network with the following architecture:
conv - relu - 2x2 max pool - linear - relu - linear - softmax
The network operates on minibatches of data that have shape (N, C, H, W)
consisting of N images, each with height H and width W and with C input
channels.
"""
def __init__(self, input_dims=(3, 32, 32), num_filters=32, filter_size=7,
hidden_dim=100, num_classes=10, weight_scale=1e-3, reg=0.0,
dtype=torch.float, device='cpu'):
"""
Initialize a new network.
Inputs:
- input_dims: Tuple (C, H, W) giving size of input data
- num_filters: Number of filters to use in the convolutional layer
- filter_size: Width/height of filters to use in the convolutional layer
- hidden_dim: Number of units to use in the fully-connected hidden layer
- num_classes: Number of scores to produce from the final linear layer.
- weight_scale: Scalar giving standard deviation for random initialization
of weights.
- reg: Scalar giving L2 regularization strength
- dtype: A torch data type object; all computations will be performed using
this datatype. float is faster but less accurate, so you should use
double for numeric gradient checking.
- device: device to use for computation. 'cpu' or 'cuda'
"""
self.params = {}
self.reg = reg
self.dtype = dtype
############################################################################
# TODO: Initialize weights and biases for the three-layer convolutional #
# network. Weights should be initialized from a Gaussian centered at 0.0 #
# with standard deviation equal to weight_scale; biases should be #
# initialized to zero. All weights and biases should be stored in the #
# dictionary self.params. Store weights and biases for the convolutional #
# layer using the keys 'W1' and 'b1'; use keys 'W2' and 'b2' for the #
# weights and biases of the hidden linear layer, and keys 'W3' and 'b3' #
# for the weights and biases of the output linear layer. #
# #
# IMPORTANT: For this assignment, you can assume that the padding #
# and stride of the first convolutional layer are chosen so that #
# **the width and height of the input are preserved**. Take a look at #
# the start of the loss() function to see how that happens. #
############################################################################
conv_param = {'stride': 1, 'pad': (filter_size - 1) // 2}
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
C, H, W = input_dims
HH = filter_size
WW = filter_size
conv_Hout = 1 + (H + 2 * conv_param['pad'] - HH) // conv_param['stride']
conv_Wout = 1 + (W + 2 * conv_param['pad'] - WW) // conv_param['stride']
pool_Hout = 1 + (conv_Hout - pool_param['pool_height']) // pool_param['stride']
pool_Wout = 1 + (conv_Wout - pool_param['pool_width']) // pool_param['stride']
self.params['W1'] = torch.normal(0.0, weight_scale, (num_filters, C, filter_size, filter_size), dtype = dtype, device = device)
self.params['b1'] = torch.zeros(num_filters, dtype = dtype, device = device)
self.params['W2'] = torch.normal(0.0, weight_scale, (num_filters * pool_Hout * pool_Wout, hidden_dim), dtype = dtype, device = device)
self.params['b2'] = torch.zeros(hidden_dim, dtype = dtype, device = device)
self.params['W3'] = torch.normal(0.0, weight_scale, (hidden_dim, num_classes), dtype = dtype, device = device)
self.params['b3'] = torch.zeros(num_classes, dtype = dtype, device = device)
############################################################################
# END OF YOUR CODE #
############################################################################다음으로는 conv - relu - max pooling - linear - relu - linear - softmax로 구성된 ThreeLayerConvNet을 구현해야 한다.
먼저 초기화는 클래스에서 사용되는 weight과 bias를 각각이 적용되는 레이어의 크기에 맞추어
weight은 weight scale만큼의 가우시안 분포를 따르는 값으로, bias는 0으로 초기화하면 된다.
def loss(self, X, y=None):
"""
Evaluate loss and gradient for the three-layer convolutional network.
Input / output: Same API as TwoLayerNet.
"""
X = X.to(self.dtype)
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
W3, b3 = self.params['W3'], self.params['b3']
# pass conv_param to the forward pass for the convolutional layer
# Padding and stride chosen to preserve the input spatial size
filter_size = W1.shape[2]
conv_param = {'stride': 1, 'pad': (filter_size - 1) // 2}
# pass pool_param to the forward pass for the max-pooling layer
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
scores = None
############################################################################
# TODO: Implement the forward pass for the three-layer convolutional net, #
# computing the class scores for X and storing them in the scores #
# variable. #
# #
# Remember you can use the functions defined in your implementation above. #
############################################################################
# Replace "pass" statement with your code
CRP_out, CRP_cache = Conv_ReLU_Pool.forward(X, W1, b1, conv_param, pool_param)
LR_out, LR_cache = Linear_ReLU.forward(CRP_out, W2, b2)
scores, L_cache = Linear.forward(LR_out, W3, b3)
############################################################################
# END OF YOUR CODE #
############################################################################
if y is None:
return scores
loss, grads = 0.0, {}
############################################################################
# TODO: Implement the backward pass for the three-layer convolutional net, #
# storing the loss and gradients in the loss and grads variables. Compute #
# data loss using softmax, and make sure that grads[k] holds the gradients #
# for self.params[k]. Don't forget to add L2 regularization! #
# #
# NOTE: To ensure that your implementation matches ours and you pass the #
# automated tests, make sure that your L2 regularization does not include #
# a factor of 0.5 #
############################################################################
# Replace "pass" statement with your code
loss, dout = softmax_loss(scores, y)
for i in range(1,4):
loss += (self.params['W' + str(i)] ** 2).sum() * self.reg
dL, grads['W3'], grads['b3'] = Linear.backward(dout, L_cache)
grads['W3'] += 2 * W3.sum() * self.reg
dLR, grads['W2'], grads['b2'] = Linear_ReLU.backward(dL, LR_cache)
grads['W2'] += 2 * W2.sum() * self.reg
dCRP, grads['W1'], grads['b1'] = Conv_ReLU_Pool.backward(dLR, CRP_cache)
grads['W1'] += 2 * W1.sum() * self.reg
############################################################################
# END OF YOUR CODE #
############################################################################
return loss, grads이어서 forward pass와 backward pass가 진행되는 loss 메소드를 구현해야 하는데, forward pass와 backward pass 모두
각 레이어 클래스의 forward와 backward 메소드를 사용하면 쉽게 할 수 있다. 또한 loss도 softmax_loss를 이용하면
무난히 구현 가능하다. 단, 주석에 나온 대로 L2 regularization을 잊지 말고 적용해야 한다.
그런데 솔직히 내가 맞게 한 게 맞는지 모르겠다. sanity check 같은 건 통과하는데
Train the net 파트에서 train acc가 50% 넘어야 한다는데, weight scale을 0.001에서 0.03으로 수정 안 하면
39% 즈음 밖에 안 나온다... 아무리 코드 봐도 매크로 레이어는 이미 구현된 거 가져다 쓰는 거라서 딱히 틀릴 게 없는데
train acc 100%로 오버핏 시키는 것도 잘만 되는데 1 epoch만 train 시키는 거만 잘 안된다 ㅜㅜ
class DeepConvNet(object):
"""
A convolutional neural network with an arbitrary number of convolutional
layers in VGG-Net style. All convolution layers will use kernel size 3 and
padding 1 to preserve the feature map size, and all pooling layers will be
max pooling layers with 2x2 receptive fields and a stride of 2 to halve the
size of the feature map.
The network will have the following architecture:
{conv - [batchnorm?] - relu - [pool?]} x (L - 1) - linear
Each {...} structure is a "macro layer" consisting of a convolution layer,
an optional batch normalization layer, a ReLU nonlinearity, and an optional
pooling layer. After L-1 such macro layers, a single fully-connected layer
is used to predict the class scores.
The network operates on minibatches of data that have shape (N, C, H, W)
consisting of N images, each with height H and width W and with C input
channels.
"""
def __init__(self, input_dims=(3, 32, 32),
num_filters=[8, 8, 8, 8, 8],
max_pools=[0, 1, 2, 3, 4],
batchnorm=False,
num_classes=10, weight_scale=1e-3, reg=0.0,
weight_initializer=None,
dtype=torch.float, device='cpu'):
"""
Initialize a new network.
Inputs:
- input_dims: Tuple (C, H, W) giving size of input data
- num_filters: List of length (L - 1) giving the number of convolutional
filters to use in each macro layer.
- max_pools: List of integers giving the indices of the macro layers that
should have max pooling (zero-indexed).
- batchnorm: Whether to include batch normalization in each macro layer
- num_classes: Number of scores to produce from the final linear layer.
- weight_scale: Scalar giving standard deviation for random initialization
of weights, or the string "kaiming" to use Kaiming initialization instead
- reg: Scalar giving L2 regularization strength. L2 regularization should
only be applied to convolutional and fully-connected weight matrices;
it should not be applied to biases or to batchnorm scale and shifts.
- dtype: A torch data type object; all computations will be performed using
this datatype. float is faster but less accurate, so you should use
double for numeric gradient checking.
- device: device to use for computation. 'cpu' or 'cuda'
"""
self.params = {}
self.num_layers = len(num_filters)+1
self.max_pools = max_pools
self.batchnorm = batchnorm
self.reg = reg
self.dtype = dtype
if device == 'cuda':
device = 'cuda:0'
############################################################################
# TODO: Initialize the parameters for the DeepConvNet. All weights, #
# biases, and batchnorm scale and shift parameters should be stored in the #
# dictionary self.params. #
# #
# Weights for conv and fully-connected layers should be initialized #
# according to weight_scale. Biases should be initialized to zero. #
# Batchnorm scale (gamma) and shift (beta) parameters should be initilized #
# to ones and zeros respectively. #
############################################################################
# Replace "pass" statement with your code
filter_size = HH = WW = 3
conv_param = {'stride': 1, 'pad': (filter_size - 1) // 2}
pool_param = {'pool_height' : 2, 'pool_width' : 2, 'stride' : 2}
prev_filters, Hout, Wout = input_dims
for i,num_filter in enumerate(num_filters):
Hout = 1 + (Hout + 2 * conv_param['pad'] - HH) // conv_param['stride']
Wout = 1 + (Wout + 2 * conv_param['pad'] - WW) // conv_param['stride']
if self.batchnorm:
self.params['gamma' + str(i)] = torch.zeros((num_filter), dtype = dtype, device = device) + 1
self.params['beta' + str(i)] = torch.zeros((num_filter), dtype = dtype, device = device)
if i in max_pools:
Hout = 1 + (Hout - pool_param['pool_height']) // pool_param['stride']
Wout = 1 + (Wout - pool_param['pool_width']) // pool_param['stride']
if weight_scale == 'kaiming':
self.params['W' + str(i)] = kaiming_initializer(num_filter, prev_filters, K = filter_size, relu = True, dtype = dtype, device = device)
else:
self.params['W' + str(i)] = torch.normal(0.0, weight_scale, (num_filter, prev_filters, HH, WW), dtype = dtype, device = device)
self.params['b' + str(i)] = torch.zeros(num_filter, dtype = dtype, device = device)
prev_filters = num_filter
i += 1
if weight_scale == 'kaiming':
self.params['W' + str(i)] = kaiming_initializer(num_filter * Hout * Wout, num_classes, dtype = dtype, device = device)
else:
self.params['W' + str(i)] = torch.normal(0.0, weight_scale, (num_filter * Hout * Wout, num_classes), dtype = dtype, device = device)
self.params['b' + str(i)] = torch.zeros(num_classes, dtype = dtype, device = device)
############################################################################
# END OF YOUR CODE #
############################################################################
# With batch normalization we need to keep track of running means and
# variances, so we need to pass a special bn_param object to each batch
# normalization layer. You should pass self.bn_params[0] to the forward pass
# of the first batch normalization layer, self.bn_params[1] to the forward
# pass of the second batch normalization layer, etc.
self.bn_params = []
if self.batchnorm:
self.bn_params = [{'mode': 'train'} for _ in range(len(num_filters))]
# Check that we got the right number of parameters
if not self.batchnorm:
params_per_macro_layer = 2 # weight and bias
else:
params_per_macro_layer = 4 # weight, bias, scale, shift
num_params = params_per_macro_layer * len(num_filters) + 2
msg = 'self.params has the wrong number of elements. Got %d; expected %d'
msg = msg % (len(self.params), num_params)
assert len(self.params) == num_params, msg
# Check that all parameters have the correct device and dtype:
for k, param in self.params.items():
msg = 'param "%s" has device %r; should be %r' % (k, param.device, device)
assert param.device == torch.device(device), msg
msg = 'param "%s" has dtype %r; should be %r' % (k, param.dtype, dtype)
assert param.dtype == dtype, msg어쨌든 지금부터는 ThreeLayerConvNet보다 더 많은 레이어를 사용된 VGG 스타일의 DeepConvNet을 구현할 것이다.
그리고 이 모델에서는 마지막 Linear 레이어를 제외하고 Conv - batchnorm - relu - pool를 하나의 레이어로 취급하는 '매크로 레이어'로 사용한다.
그래서 각종 parameter를 초기화할 때도 for문을 돌면서 Batch Normalization과 Max-pooling을 적용받는 레이어에서는 Conv 레이어와 동시에 초기화해주어야 한다. 그리고 여기서 Batch Normalization고 kaiming intializizer를 사용했는데,
Assignment #3-1에서 Dropout을 무시했던 것처럼 추후에 구현할 것이니 무시하고 넘어가면 된다.
def loss(self, X, y=None):
"""
Evaluate loss and gradient for the deep convolutional network.
Input / output: Same API as ThreeLayerConvNet.
"""
X = X.to(self.dtype)
mode = 'test' if y is None else 'train'
# Set train/test mode for batchnorm params since they
# behave differently during training and testing.
if self.batchnorm:
for bn_param in self.bn_params:
bn_param['mode'] = mode
scores = None
# pass conv_param to the forward pass for the convolutional layer
# Padding and stride chosen to preserve the input spatial size
filter_size = 3
conv_param = {'stride': 1, 'pad': (filter_size - 1) // 2}
# pass pool_param to the forward pass for the max-pooling layer
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
scores = None
############################################################################
# TODO: Implement the forward pass for the DeepConvNet, computing the #
# class scores for X and storing them in the scores variable. #
# #
# You should use the fast versions of convolution and max pooling layers, #
# or the convolutional sandwich layers, to simplify your implementation. #
############################################################################
# Replace "pass" statement with your code
cache = {}
out = X
for i in range(self.num_layers - 1):
if i in self.max_pools:
if self.batchnorm:
out, cache[str(i)] = Conv_BatchNorm_ReLU_Pool.forward(out, self.params['W'+str(i)], self.params['b' + str(i)], self.params['gamma' + str(i)],
self.params['beta' + str(i)], conv_param, self.bn_params[i], pool_param)
else:
out, cache[str(i)] = Conv_ReLU_Pool.forward(out, self.params['W' + str(i)], self.params['b' + str(i)], conv_param, pool_param)
else:
if self.batchnorm:
out, cache[str(i)] = Conv_BatchNorm_ReLU.forward(out, self.params['W'+str(i)], self.params['b' + str(i)], self.params['gamma' + str(i)],
self.params['beta' + str(i)], conv_param, self.bn_params[i])
else:
out, cache[str(i)] = Conv_ReLU.forward(out, self.params['W' + str(i)], self.params['b' + str(i)], conv_param)
i += 1
out, cache[str(i)] = Linear.forward(out, self.params['W' + str(i)], self.params['b' + str(i)])
scores = out
############################################################################
# END OF YOUR CODE #
############################################################################
if y is None:
return scores
loss, grads = 0, {}
############################################################################
# TODO: Implement the backward pass for the DeepConvNet, storing the loss #
# and gradients in the loss and grads variables. Compute data loss using #
# softmax, and make sure that grads[k] holds the gradients for #
# self.params[k]. Don't forget to add L2 regularization! #
# #
# NOTE: To ensure that your implementation matches ours and you pass the #
# automated tests, make sure that your L2 regularization does not include #
# a factor of 0.5 #
############################################################################
# Replace "pass" statement with your code
loss, up_grad = softmax_loss(scores, y)
for i in range(self.num_layers):
loss += (self.params['W' + str(i)] ** 2).sum() * self.reg
up_grad, dw, grads['b' + str(i)] = Linear.backward(up_grad, cache[str(i)])
grads['W' + str(i)] = dw + 2 * self.params['W' + str(i)] * self.reg
for i in range(i - 1, -1, -1):
if i in self.max_pools:
if self.batchnorm:
up_grad, dw, grads['b' + str(i)], dgamma, grads['beta' + str(i)] = Conv_BatchNorm_ReLU_Pool.backward(up_grad, cache[str(i)])
grads['gamma' + str(i)] = dgamma + 2 * self.params['gamma' + str(i)] * self.reg
else:
up_grad, dw, grads['b' + str(i)] = Conv_ReLU_Pool.backward(up_grad, cache[str(i)])
grads['W' + str(i)] = dw + 2 * self.params['W' + str(i)] * self.reg
else:
if self.batchnorm:
up_grad, dw, grads['b' + str(i)], dgamma, grads['beta' + str(i)] = Conv_BatchNorm_ReLU.backward(up_grad, cache[str(i)])
grads['gamma' + str(i)] = dgamma + 2 * self.params['gamma' + str(i)] * self.reg
else:
up_grad, dw, grads['b' + str(i)] = Conv_ReLU.backward(up_grad, cache[str(i)])
grads['W' + str(i)] = dw + 2 * self.params['W' + str(i)] * self.reg
############################################################################
# END OF YOUR CODE #
############################################################################
return loss, grads이번에도 loss 메소드에서 forwad pass와 backward pass를 진행하는데, forward pass는 이전처럼 각 레이어 클래스의 forward 메소드를 이용하여 forward pass를 진행한다. 이때 Conv 레이어, Pooling 레이어 별개로 사용하는 것이
아니라 초기화할 때처럼 매크로 레이어를 사용해서 Pooling을 사용하면 Conv_ReLU_Pool 클래스를, 사용하지 않으면 Conv_ReLU 클래스를 사용하는 식으로 구현하면 된다.
마찬가지로 backward pass 과정도 매크로 레이어를 이용한다.
또한 여기서도 batch normalization이 사용되었는데 초기화할 때처럼 일단은 무시하고 넘어가자
def find_overfit_parameters():
weight_scale = 2e-3 # Experiment with this!
learning_rate = 1e-5 # Experiment with this!
############################################################################
# TODO: Change weight_scale and learning_rate so your model achieves 100% #
# training accuracy within 30 epochs. #
############################################################################
# Replace "pass" statement with your code
weight_scale = 1e-1
learning_rate = 1e-3
############################################################################
# END OF YOUR CODE #
############################################################################
return weight_scale, learning_rate그리고 DeepConvNet에서 50개의 이미지에 대하여 오버핏이 되는 weight scale과 learning rate를 찾으면 되는데
대충 값 넣어 보면 금방 할 수 있을 것이다.
def kaiming_initializer(Din, Dout, K=None, relu=True, device='cpu',
dtype=torch.float32):
"""
Implement Kaiming initialization for linear and convolution layers.
Inputs:
- Din, Dout: Integers giving the number of input and output dimensions for
this layer
- K: If K is None, then initialize weights for a linear layer with Din input
dimensions and Dout output dimensions. Otherwise if K is a nonnegative
integer then initialize the weights for a convolution layer with Din input
channels, Dout output channels, and a kernel size of KxK.
- relu: If ReLU=True, then initialize weights with a gain of 2 to account for
a ReLU nonlinearity (Kaiming initializaiton); otherwise initialize weights
with a gain of 1 (Xavier initialization).
- device, dtype: The device and datatype for the output tensor.
Returns:
- weight: A torch Tensor giving initialized weights for this layer. For a
linear layer it should have shape (Din, Dout); for a convolution layer it
should have shape (Dout, Din, K, K).
"""
gain = 2. if relu else 1.
weight = None
if K is None:
###########################################################################
# TODO: Implement Kaiming initialization for linear layer. #
# The weight scale is sqrt(gain / fan_in), #
# where gain is 2 if ReLU is followed by the layer, or 1 if not, #
# and fan_in = num_in_channels (= Din). #
# The output should be a tensor in the designated size, dtype, and device.#
###########################################################################
# Replace "pass" statement with your code
weight_scale = gain / Din
weight = torch.normal(0.0, weight_scale, (Din, Dout), dtype = dtype, device = device)
###########################################################################
# END OF YOUR CODE #
###########################################################################
else:
###########################################################################
# TODO: Implement Kaiming initialization for convolutional layer. #
# The weight scale is sqrt(gain / fan_in), #
# where gain is 2 if ReLU is followed by the layer, or 1 if not, #
# and fan_in = num_in_channels (= Din) * K * K #
# The output should be a tensor in the designated size, dtype, and device.#
###########################################################################
# Replace "pass" statement with your code
weight_scale = gain / (Din * K * K)
weight = torch.normal(0.0, weight_scale, (Din, Dout, K, K), dtype = dtype, device = device)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return weight드디어 앞에서 언급되었던 kaiming_initializer를 구현한다. kaiming initializer는 해당 레이어에서의 input과 output의
분산을 동일하게 하려고 사용하는 initializer로 weight scale을 gain / n 만큼 정해준다.
gain의 경우 ReLU 레이어의 경우 2, 아니면 1로 사전에 정해주었으니, 우리는 n을 정해주어야 하는데,
Conv 레이어에서는 n = Din * k * k이며, Linear 레이어에서는 n = Din이다.
def create_convolutional_solver_instance(data_dict, dtype, device):
model = None
solver = None
################################################################################
# TODO: Train the best DeepConvNet that you can on CIFAR-10 within 60 seconds. #
################################################################################
# Replace "pass" statement with your code
input_dims = data_dict['X_train'].shape[1:]
num_classes = len(data_dict['y_train'].unique())
weight_scale = 'kaiming'
model = DeepConvNet(input_dims=input_dims, num_classes=10,
num_filters=[16,32,64],
max_pools=[0,1,2],
weight_scale=weight_scale,
reg=1e-5,
dtype=dtype,
device=device
)
solver = Solver(model, data_dict,
num_epochs=200, batch_size=1024,
update_rule=adam,
optim_config={
'learning_rate': 3e-3
}, lr_decay = 0.999,
print_every=1000, device=device)
################################################################################
# END OF YOUR CODE #
################################################################################
return solver이어서 DeepConvNet을 테스트하는 create_convolutional_slover_instance를 구현해야 한다.
제대로 구현하면 최소한 71%의 val acc와 70%의 test acc를 얻어야 하는데
train acc는 잘만 오르는데, val acc는 69, 68%에서 벽이라도 있는지 올리기 정말 힘들었다.
결국 val acc 72%, test acc 71%가 나오는 hyper parameter 찾았는데, 이것도 매번 나오는 건 아니고,
운 없으면 69, 68%까지 떨어진다. 이 부분 구현하는 게 Assignment #3 나머지 전체보다 더 걸린 거 같다 ㅜㅜ
class BatchNorm(object):
@staticmethod
def forward(x, gamma, beta, bn_param):
"""
Forward pass for batch normalization.
During training the sample mean and (uncorrected) sample variance are
computed from minibatch statistics and used to normalize the incoming data.
During training we also keep an exponentially decaying running mean of the
mean and variance of each feature, and these averages are used to normalize
data at test-time.
At each timestep we update the running averages for mean and variance using
an exponential decay based on the momentum parameter:
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
Note that the batch normalization paper suggests a different test-time
behavior: they compute sample mean and variance for each feature using a
large number of training images rather than using a running average. For
this implementation we have chosen to use running averages instead since
they do not require an additional estimation step; the PyTorch
implementation of batch normalization also uses running averages.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', torch.zeros(D, dtype=x.dtype, device=x.device))
running_var = bn_param.get('running_var', torch.zeros(D, dtype=x.dtype, device=x.device))
out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# #
# You should store the output in the variable out. Any intermediates #
# that you need for the backward pass should be stored in the cache #
# variable. #
# #
# You should also use your computed sample mean and variance together #
# with the momentum variable to update the running mean and running #
# variance, storing your result in the running_mean and running_var #
# variables. #
# #
# Note that though you should be keeping track of the running #
# variance, you should normalize the data based on the standard #
# deviation (square root of variance) instead! #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
#######################################################################
# Replace "pass" statement with your code
mean = 1 / N * x.sum(axis = 0)
running_mean = momentum * running_mean + (1 - momentum) * mean
x_mean = x - mean
var = 1 / N * (x_mean ** 2).sum(axis = 0)
running_var = momentum * running_var + (1 - momentum) * var
std = (var + eps).sqrt()
istd = 1 / std
x_hat = x_mean * istd
out = gamma * x_hat + beta
cache = (x_hat, gamma, x_mean, istd, std, var, eps)
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
# Replace "pass" statement with your code
normalized = (x - running_mean) / (running_var + eps) ** 0.5
out = normalized * gamma + beta
#######################################################################
# END OF YOUR CODE #
#######################################################################
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean.detach()
bn_param['running_var'] = running_var.detach()
return out, cache@staticmethod
def backward(dout, cache):
"""
Backward pass for batch normalization.
For this implementation, you should write out a computation graph for
batch normalization on paper and propagate gradients backward through
intermediate nodes.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
# Don't forget to implement train and test mode separately. #
###########################################################################
# Replace "pass" statement with your code
x_hat, gamma, x_mean, istd, std, var, eps = cache
m = dout.shape[0]
dbeta = dout.sum(axis = 0)
dgamma = (dout * x_hat).sum(axis = 0)
dx_hat = dout * gamma
dvar = (dx_hat * x_mean * (-0.5) * (var + eps) ** (-3 / 2)).sum(axis = 0)
dmean = dx_hat.sum(axis = 0) * (- istd) + dvar * -2 * x_mean.sum(axis = 0) / m
dx = dx_hat * istd + dvar * 2 * x_mean / m + dmean / m
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta이제 마지막으로 Batch Normalization 부분이다.

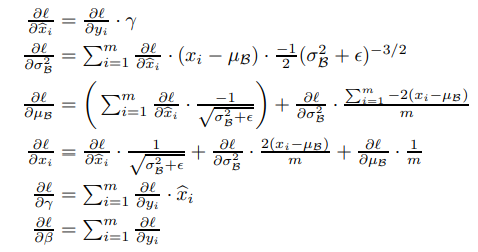
어려울 것 없이 forward, backwad 모두 논문에 잘 나와있으니 그거 보고 따라 하면 된다.
좌측이 forward, 우측이 backward 전개 과정이다.
@staticmethod
def backward_alt(dout, cache):
"""
Alternative backward pass for batch normalization.
For this implementation you should work out the derivatives for the batch
normalizaton backward pass on paper and simplify as much as possible. You
should be able to derive a simple expression for the backward pass.
See the jupyter notebook for more hints.
Note: This implementation should expect to receive the same cache variable
as batchnorm_backward, but might not use all of the values in the cache.
Inputs / outputs: Same as batchnorm_backward
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# #
# After computing the gradient with respect to the centered inputs, you #
# should be able to compute gradients with respect to the inputs in a #
# single statement; our implementation fits on a single 80-character line.#
###########################################################################
# Replace "pass" statement with your code
x_hat, gamma, x_mean, istd, std, var, eps = cache
m = dout.shape[0]
# y = gamma * x_hat + beta
dbeta = dout.sum(axis = 0)
dgamma = (x_hat * dout).sum(axis = 0)
dx = gamma * istd * (m * dout - dgamma * x_hat - dbeta) / m
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta그리고 논문의 backward pass 과정을 조금 더 간편화 한 버전을 구현하는데, 이 부분은 도저히 못하겠어서
구글링 해서 전개 과정을 찾아보고 겨우 했다.
https://costapt.github.io/2016/07/09/batch-norm-alt/
위 링크에 들어가면 어떻게 효율적인 batch norm이 구현되는지 차근차근 식을 전개해 나간다.
class SpatialBatchNorm(object):
@staticmethod
def forward(x, gamma, beta, bn_param):
"""
Computes the forward pass for spatial batch normalization.
Inputs:
- x: Input data of shape (N, C, H, W)
- gamma: Scale parameter, of shape (C,)
- beta: Shift parameter, of shape (C,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance. momentum=0 means that
old information is discarded completely at every time step, while
momentum=1 means that new information is never incorporated. The
default of momentum=0.9 should work well in most situations.
- running_mean: Array of shape (C,) giving running mean of features
- running_var Array of shape (C,) giving running variance of features
Returns a tuple of:
- out: Output data, of shape (N, C, H, W)
- cache: Values needed for the backward pass
"""
out, cache = None, None
###########################################################################
# TODO: Implement the forward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
# Replace "pass" statement with your code
N,C,H,W = x.shape
m = x.permute(1,0,2,3).reshape(C, -1).T
out, cache = BatchNorm.forward(m, gamma, beta, bn_param)
out = out.T.reshape(C, N, H, W).permute(1,0,2,3)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return out, cache
@staticmethod
def backward(dout, cache):
"""
Computes the backward pass for spatial batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
# Replace "pass" statement with your code
N, C, H, W = dout.shape
m = dout.permute(1,0,2,3).reshape(C,-1).T
dx, dgamma, dbeta = BatchNorm.backward_alt(m, cache)
dx = dx.T.reshape(C, N, H, W).permute(1, 0, 2, 3)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta추가로 spatial batch normalization도 구현하는데
이거는 permute 기능을 이용해서 x의 구조를 변경한 후, 기존의 BatchNorm의 forward와 backward를 이용하면
쉽게 할 수 있다.
========================================================================
드디어 미루고 미뤘던 Assignment #3 포스팅을 끝냈다
근데 벌써 Assignment #4 하러 가야 한다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ
'Deep Learning for Computer Vision' 카테고리의 다른 글
| EECS 498-007 / 598-005 Lecture 11 : Training Neural Networks (Part 2) (0) | 2022.01.26 |
|---|---|
| 빠르면 연말부터 이어서 포스팅할게요 ㅜㅜ (0) | 2021.11.25 |
| EECS 498-007 / 598-005 Assignment #3-1 (0) | 2021.02.03 |
| EECS 498-007 / 598-005 Lecture 10 : Training Neural Networks (Part 1) (0) | 2021.02.02 |
| EECS 498-007 / 598-005 Lecture 9 : Hardware and Software (0) | 2021.01.28 |


