강의 링크
https://www.youtube.com/watch?v=ANyxBVxmdZ0&list=PL5-TkQAfAZFbzxjBHtzdVCWE0Zbhomg7r&index=7
강의 슬라이드
https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture07.pdf

지금까지는 다차원 배열로 구성된 이미지를 벡터로 만들어서 처리했는데, 이 과정에서 spatial structure는
사라지게 되었다. 그래서 이번 시간에는 spatial structure를 처리할 수 있는 Convolutional Network에 대해
배워볼 것이다.

Convolutional Network는 기존에 배웠던 Fully-Connected Layers와 Activation Function 외에도 Convolution Layers, Pooling Layers, Normalization을 가지고 있는 Network이다.

기존에 배웠던 Fully-Connected Layer에서는 입력으로 받은 다차원의 이미지를 하나의 벡터로 만들어서 사용했는데,

Convolution Layer에서는 입력을 별다른 가공 없이 그대로 사용해서 spatial structure가 보존된다. 그리고 Convolutional Layer에서의 weight은 filter라고 불리며

fiter는 input matrix 위를 'slide'하며 filter와 접해 있는 matrix 영역과의 내적을 통해서 filter와 해당 영역이 얼마나
일치하는지를 나타내는 scalar 값을 만들어낸다.

filter가 input matrix 전체를 slide 하면 filter와의 연산의 결과로 만들어진 matrix가 하나 나오는데
이것을 activation map이라고 지칭하고 각 레이어에서 filter는 여러 개 사용할 수 있으며 따라서 activation map도
여러 개 나올 수 있다. 이 과정에서 이미지 전체적인 spatial structure는 사라질 수 있지만, local spatial structure는
보존될 수 있다.

Convolution Layer를 활용하는 두 가지 관점이 있는데, 하나는 activation map이 input으로 받은 데이터가 filter와
얼마나 일치하는 지를 나타낸 것이므로 activation map을 통해 output의 spatial structure를 알 수 있다는 관점이다.
다른 하나는 output을 하나의 그리드로 여기며, 그리드의 각 지점은 feature vector로 이루어져 있어 이를 통해 input의 structure나 appearance에 대해 알게 해 준다는 관점이다.

글로만 설명하면 뜬구름 잡는 것 같기도 해서 추가적인 설명을 위해서 다른 데서 예시 슬라이드를 가져왔는데, 위
슬라이드에서는 이미지를 2가지 filter를 통해서 vertical edge와 horizaontal edge를 분리해냈다. 여기서 각각의 vertical edge 이미지와 horizontal edge 이미지는 activation map이라고 볼 수 있으며, 이 activation map들을 통해서 output에서 vertical edge는 어디에, 얼마나 존재하는지 등의 spatial structure를 확인할 수 있다. 그리고 output을 그리드로 보면 vertical edge와 horizontal edge의 정보가 담긴 feature vector가 그리드의 한 원소가 되는데, 이를 통해 input의 각
지점에서 vertical 요소와 horizontal 요소가 얼마나 존재하는지 등의 structure도 알 수 있다.

그리고 당연하게도 Convolution Layer에 Batch 개념을 접목할 수 있으며

Fully-Connected Layer를 여러 개 쌓아서 neural network를 구성하는 것처럼 Convolution Layer도 그렇게 사용하는 것이
가능하며 레이어의 수에 따라서 달리 부르는데, N개의 레이어로 구성되어 있는 경우
N Layer Convolutional Network라고 부른다. 또한 Convolution Layer는 Linear 연산을 수행하므로 NonLinearity를
위해서 Activation Function을 적용해주어야 한다.

Convolution Layer의 특징으로는 Full-Connected Layer가 입력과 동일한 이미지의 템플릿을 학습하는 것과 달리,
filter가 local template을 학습한다는 점이 있다. 그리고 output에서의 feature vector의 각 원소는 각
filter(local pattern)와 얼마나 일치하는지를 나타내는데, 이건 Hubol과 Wiesel의 연구에서 고양이가 시각적인 local pattern에 반응한 것과 비슷하다고 볼 수 있다고 한다.

Convolution Layer의 문제점으로는 레이어를 지날 때마다 feature map, 즉 데이터의 크기가 줄어든다는 문제가 있다.
그래서 feature map 가장자리에 임의의 픽셀을 추가하는 'Padding'이란 것을 해주는데, 주위 픽셀의 평균으로 추가하거나, 근처의 값의 복사하는 등 여러 가지 방법이 있지만 대부분의 경우, 그냥 0을 추가하는 'Zero Padding'이란 것을 많이
사용한다.

그리고 얼마나 Padding 할지는 Hyperparameter P에
따라 정해지는데 P가 정해지면 Input의 크기와 Filter의 크기가 각각 W, K라고 할 때 Output의 크기는
W - K + 1 + 2P가 된다. 그리고 보통 P의 값은 input과 output의 크기가 같게 되는 (K - 1) / 2로 정하며 이렇게 할 경우 'Same Padding'이라고 부른다.

Convolution Layer의 구성 요소 중 하나로는 Receptive Field란 것이 있다. Convolution Layer에서의 Output의 한 원소는 filter가 참조하는 local region의 영역의 값만 영향을 받는데, 이 local region을 'Receptive Field'라 한다.
그리고 Neural Network에서 Convolution Layer가 transitive하게 연결되어 있는 경우 해당 Layer의 Output의 원소는
그 Layer의 Input의 local region만이 아니라, 이전 Layer의 Input의 local region의 영향을 받는다라고도 할 수 있다.
그래서 Receptive Field의 의미는 고정된 것이 아니고 보통 두 개의 의미로 사용되는데, 하나는 Layer의 Input에서
영향을 받는 부분을 말하며, 다른 하나는 모델의 Input에서 영향을 받는 부분을 말한다.
또한 위 슬라이드에서 볼 수 있듯이 모델의 Input에 대한 receptive field는 Convolution Layer에 비례해 크기가
선형적으로 증가함을 볼 수 있다. 그래서 최종 Output의 한 원소가 모델 Input 이미지의 전체를 receptive field로
가지려면 수많은 레이어가 필요하다. 1024 x 1024 크기의 이미지에 3 x 3 필터를 사용하는 경우만 해도 500여 개의
레이어가 필요하다. 그래서 이를 위해 Downsampling 정도를 조절하는 hyperparameter 'stride'를 사용한다.


Stride는 필터가 Input 위로 sliding 할 때, 얼마나 slide 할 것인지, 정도를 나타내며, 보통 그 값을 S로 나타낸다.
Stride를 사용했을 시, Output의 크기는 (W - K + 2P) / S + 1이 되며 대부분의 경우 (W - K + 2P)는 S로 나누어
떨어지며, 그렇지 않은 경우는 버림 하거나 반올림을 한다고 한다.
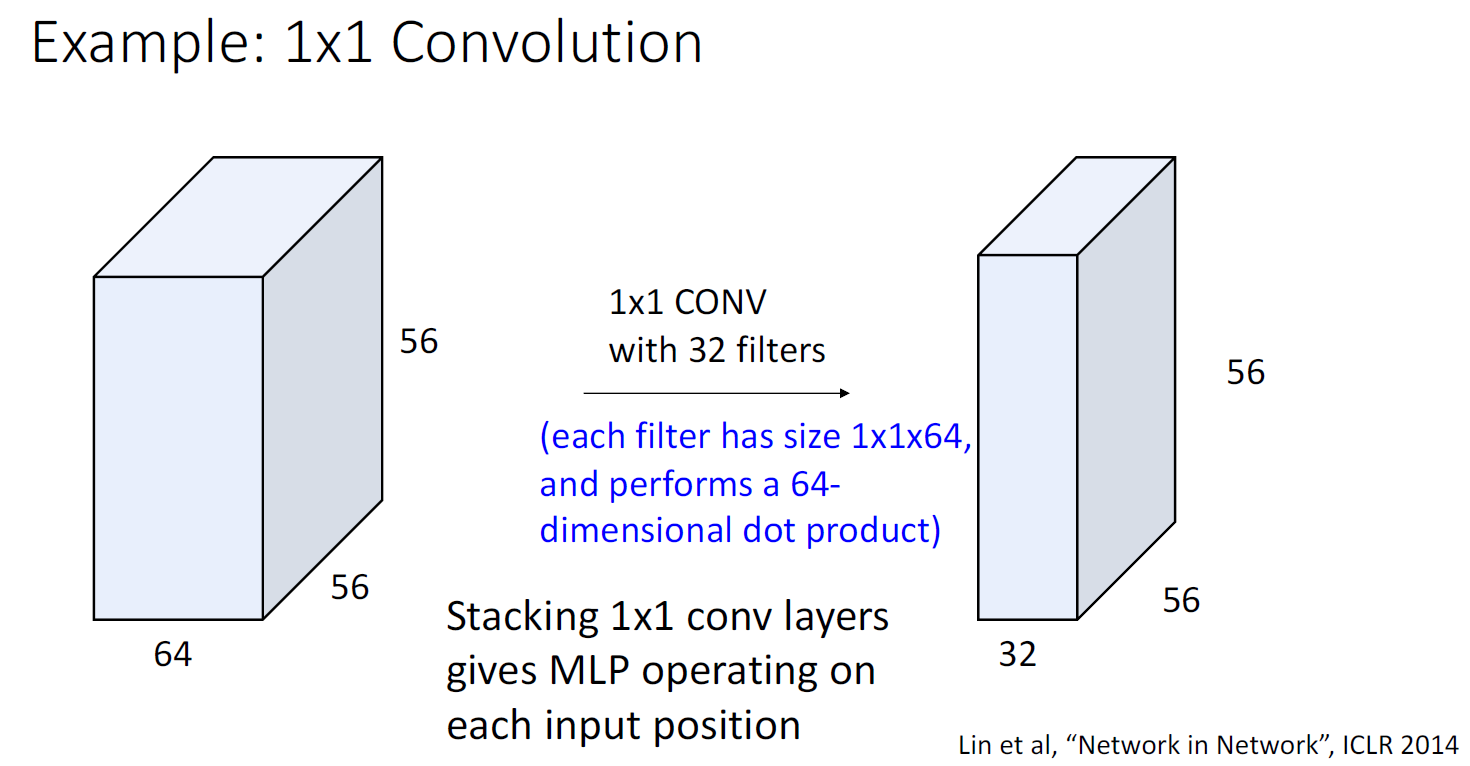
때때로 1 x 1 크기의 필터를 사용하는 경우, 각 필터는 input의 feature vector마다의 Linear Layer로 볼 수 있는데
이렇게 되면 각각의 feature vector가 input의 원소로 존재하는 Fully-Connected Neural Network로 볼 수 있다. 그래서 이런 형태로 사용되는 형태를 'Network in Network Structure'라고 부른다고 한다.
그리고 1 x 1 Convolution과 Fully-Connected Neural Network의 차이로는 전자는 spatial structure는 보존하며
input의 channel( 3 x N x M 크기인 RGB 이미지의 경우 '3'이 channel)을 변경할 때 사용하고, 후자는 데이터의 spatial structure를 없애고 하나의 벡터로 만들어 값을 만들고 싶을 때, 주로 Network의 마지막에 score를 만들고 싶을 때 사용한다고 한다.



지금까지는 2D Convolution만 다뤘지만 1D와 3D Convolution도 존재하는데,
1D는 연속적으로 존재하는 textual data나 audio data에서 사용되며 3D는 point cloud 등의 3D 데이터에서 주로
사용된다고 한다.

이제부터는 Convolutioin Layer의 'Stride' 말고도 데이터를 downsample 할 수 있는 Pooling Layer에 대해서 배울
것이다. Hyperparameter로는 Kernel Size, Stride, Pooling Function이 있는데 여기서 Pooling Function은 Kernel에서
어떻게 downsampling을 수행하는 Function을 나타낸다.
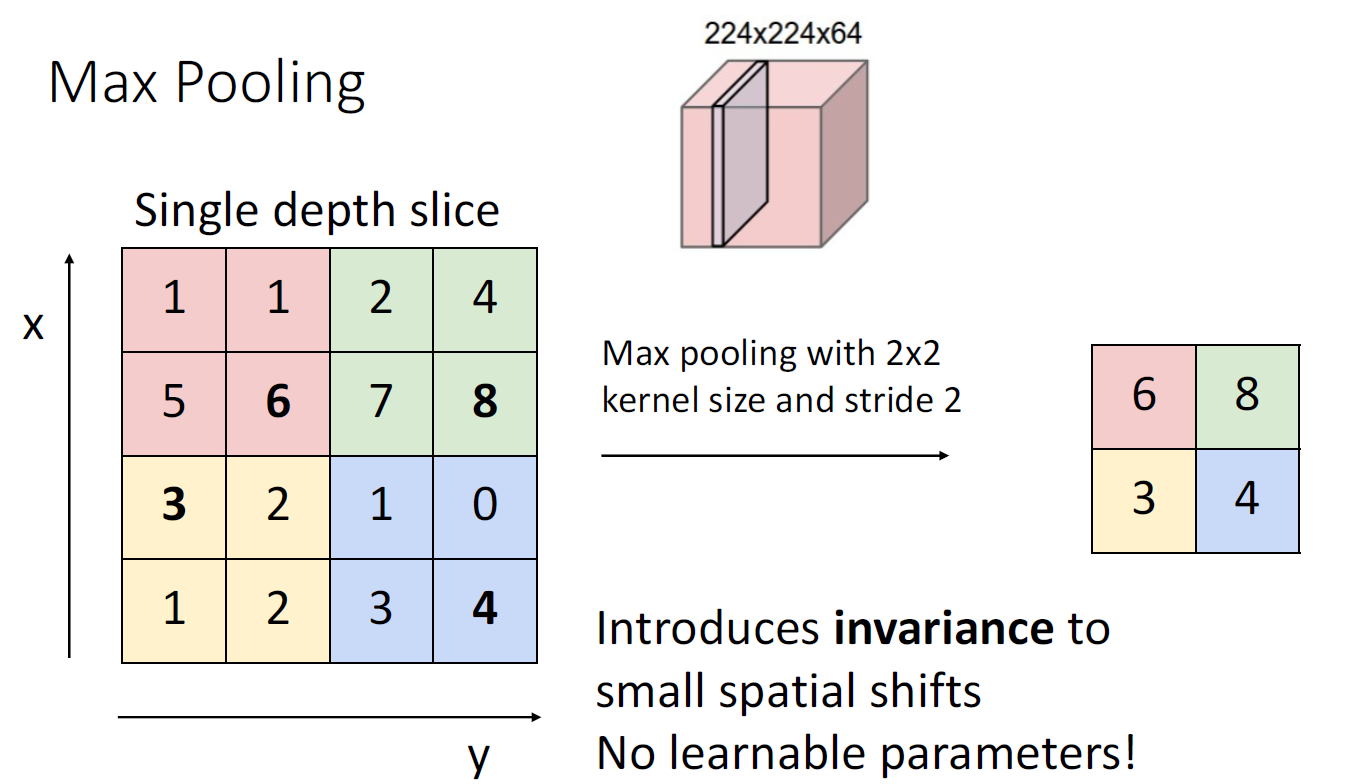
대표적인 Pooling 기법으로는 커널에서 최댓값만 남기는 Max Pooling이 있으며 그밖에도 평균값을 남기는
Average Pooling도 있다. Downsampling에서 Pooling은 Convolution Layer에서의 stride 보다 더 선호되는데,
Pooling에서는 어떠한 learnable parameter도 없으며 약간의 spatial shift에도 invariance가 보장되기 때문이다.
예를 들어 max pooling에서는 이미지에서 어떤 객체의 위치가 변경되더라도 이미지의 국소적인 부분의 변화는 그다지 변화가 없기에 pooling을 적용하는 경우에도 객체를 구성하는 커널들의 결과는 별 차이가 없다.

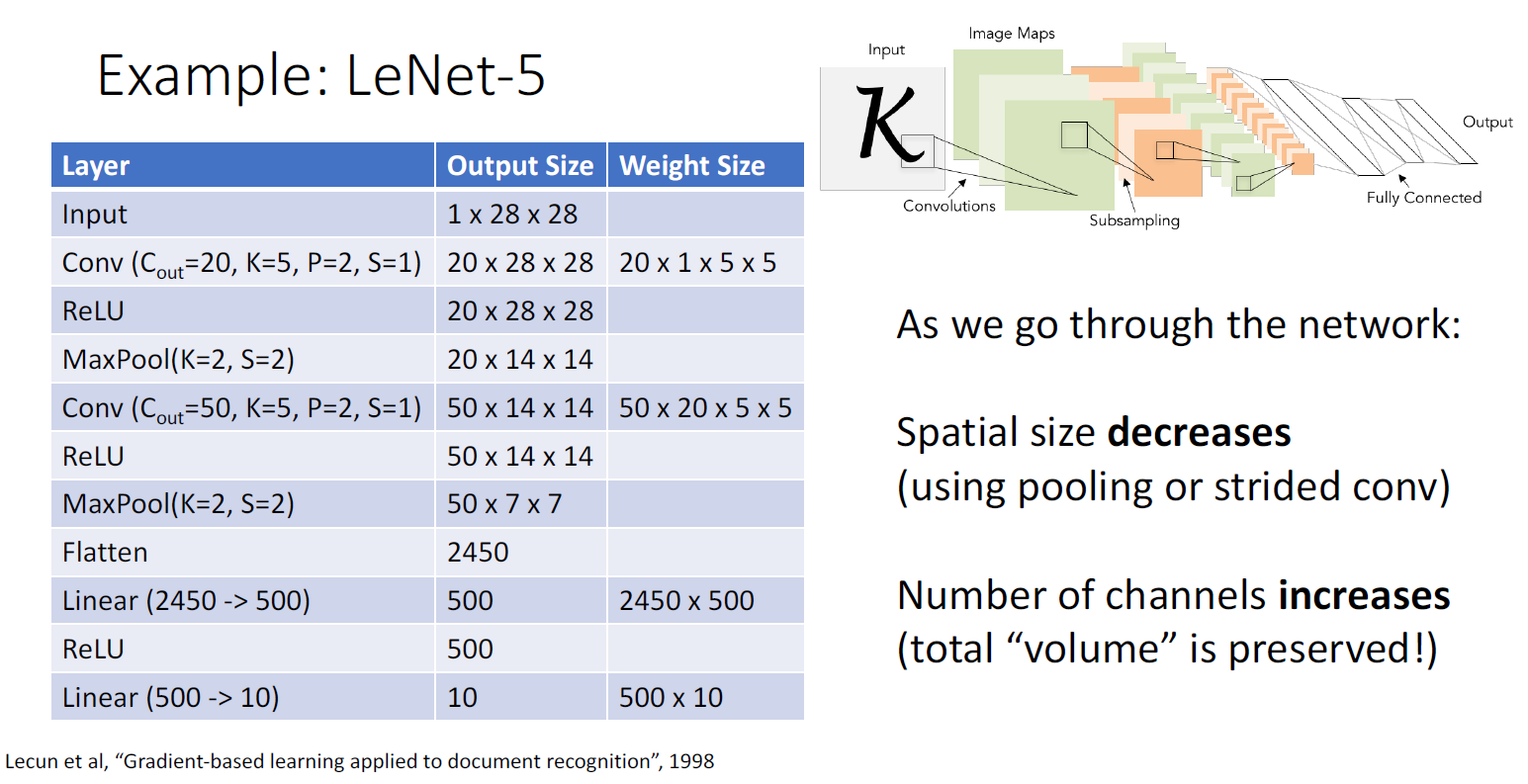
Convolutional Network의 Classic Architecture는 지금까지 배운 Convolution Layer, Pooling Layer, Fully-Connected Layer로 구성할 수 있는데, 대표적인 아키텍처로는 글자를 인식하는 작업에 사용했던 LeNet-5가 있다.
LeNet-5에서 spatial size는 감소하지만 채널의 수는 증가해서 데이터의 전체적인 크기는 유지되는 것을 볼 수 있는데,
이건 Convolutional Network의 일반적인 특징이라고 한다. 그리고 여기서는 Activation Function으로 Relu를
사용했는데, Max Pooling 자체로도 NonLinearity를 가질 수 있기에 필수는 아니라고 한다.

Convolutional Network는 근본적으로 'Deep'한 구조이기에 Global Optima로 수렴하기 쉽지 않다.
그래서 Normalization 기법을 사용하는데

대표적으로 Batch Normalization이 있다. Batch Normalization은 이전 레이어의 output을 zero mean, unit variance distribution을 가지도록 변환한다. 이 작업은 모델의 internal covariance shift를 감소시키기 위해서 수행하는 것으로
모델이 학습될 때, 각 레이어에서의 weight이 매번 동시에 optimization 되어서 해당 레이어의 output의 distribution이 변경되는데 이러한 distribution 변화는 optimization에 좋지 않다고 한다. 그래서 모든 레이어가 안정된 분포를 가지게 특정한 분포로 standardize 하는 것이라고 한다. 나름 강의 설명한 거 열심히 옮겨 봤는데 설명 자체가 뜬구름 잡는
소리인 거 같다 ㅋㅋ 아니면 내가 영어라서 못 알아들은 건가?
https://www.youtube.com/watch?v=nUUqwaxLnWs
예전에 봤던 Andrew Ng의 강의에서는 자세히 설명해줬던 기억이 나서 다시 들어봤는데, Batch Normalization에 대해
잘 설명되어있었다. 나처럼 강의가 바로 이해가 안 되면 들어보는 걸 추천한다. EECS 498-007는 대학교 강의라
그런지 구성은 좋은데 강의 시간제한으로 스킵되거나 간단히만 집고 넘어가는 게 참 아쉬운 거 같다.

Batch Normalization의 구현은 위와 같이 구현하는데 Normalize 하는 부분의 엡실론은 0으로 나누는 것을 방지하기
위해 포함된 hyperparameter인데 그다지 중요하지는 않다 그리고 Batch Normalization에서는
unit variance constraint에 모든 레이어가 fit 하는 것은 쉽지 않아서 추가적인 shift parameter를 사용한다.

하지만 이것들도 minibatch에 의존하는 변수인지라 test time에서는 train에서 했던 것처럼 할 수가 없다.

그래서 test 과정에서는 평균과 분산 모두 train 과정에서 사용했던 값의 평균으로 이용한다.

그리고 test에서 추가적 계산 없이 평균이라는 상수를 사용하기 때문에
Batch Normalization은 Linear operator로 볼 수 있게 되고, 그래서
Fully-Connected Layer나 Convolution Layer와 합쳐질 수 있다고 한다.

Batch Normalization은 Fully-connected network와 Convolutional network에서 모두 사용 가능하다는 데 두 가지
경우의 차이는 Spatial structure가 포함되는 Conv Net 특성상, Batch norm도 spatial dimension을 고려한다는 것이
있다.
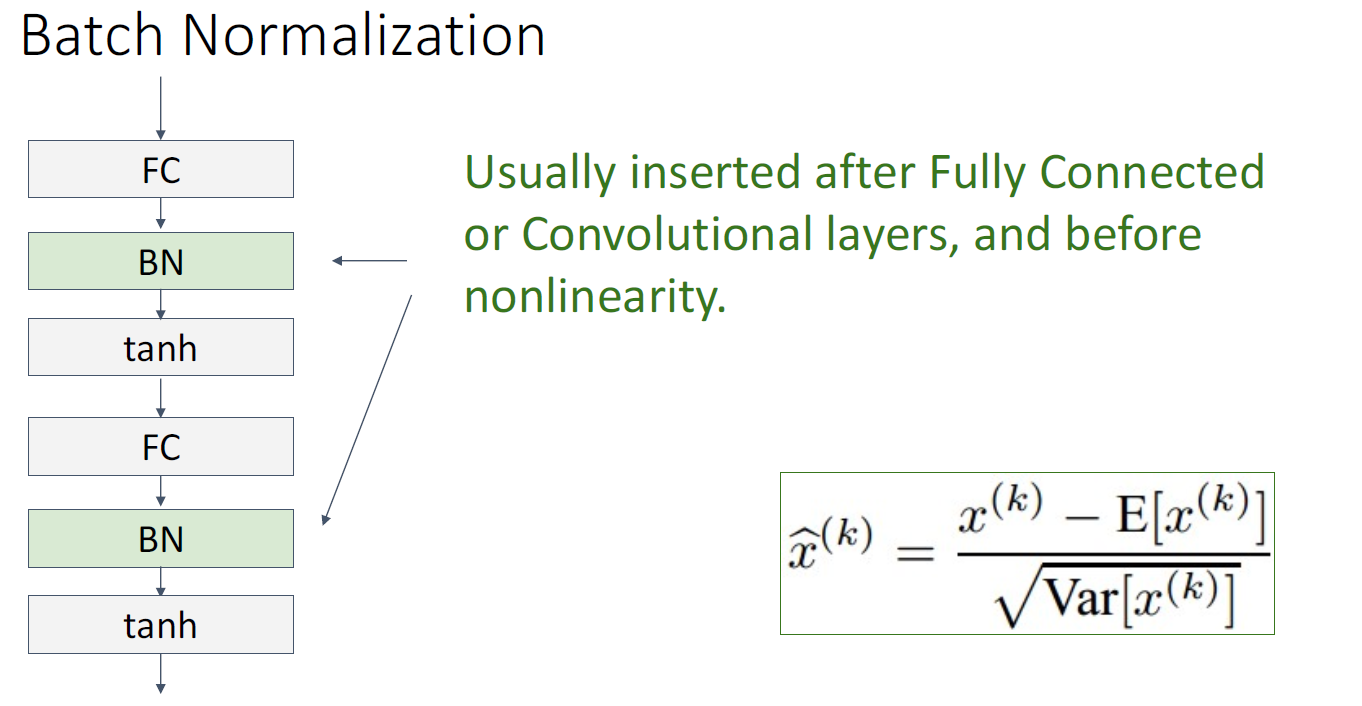

Batch Normalization은 주로 Fully Connected Layer나 Convolution Layer 다음에, Activation Function 전에 사용하는데,
Batch Norm 사용 시, 위 슬라이드에 나온 대로 여러 가지 장점들을 보여준다.

그리고 아직 Batch norm의 이론적 근거가 명확하지 않고, train과정과 test 과정이 서로 다르기에 잠재적인 버그의 가능성을 가지고 있다는 문제점도 있다.
또한 학습 데이터의 분포가 편향되는 등, 좋지 못한 분포에서는 사용 안 했을 때보다 안 좋은 성능을 보인다.

Layer Normalization은 Batch Norm의 변형으로 batch norm이 평균과 분산을 계산할 때, batch dimension에 대해서
계산했다면, layer norm은 feature dimension에 대해 계산하기에 test time에서도 문제없이 작동한다고 한다.

Batch norm의 변형으로는 Instance Normalization이란 것도 있는데 이건 이미지에서 쓰이는
일종의 layer norm의 계열로 spatial dimension에 대해서 평균과 분산을 계산한다고 한다.

여러 Normalization 기법들을 이해하기 쉽게 3D로 표현한 것으로 여기 있는 3가지 Norm 말고도

Gropu Normalization도 있는데 이건 channel dimension을
특정 group으로 나누고 이 group에 대해서 normalization을
진행하는 방식이라고 하는데 Object detection 등에서
효과를 발휘한다고 한다.

마지막으로 Convolutional Network에서 Convolution Layer가 가장 연산이 많이 필요하다고 하는데
이건 강의 시간 상 설명은 생략했다. 근데 바로 다음 강의에 설명 잘 되어있어서 따로 찾아보지 말고
그냥 그렇다고만 알면 될 듯하다.

========================================================================
한동안 딴짓 좀 했더니 8강 정리도 밀리고 Assignment 3도 해야 한다. ㅜㅜㅜㅜㅜ
너무 밀렸는데 ㅋㅋ
'Deep Learning for Computer Vision' 카테고리의 다른 글
| EECS 498-007 / 598-005 Lecture 9 : Hardware and Software (0) | 2021.01.28 |
|---|---|
| EECS 498-007 / 598-005 Lecture 8 : CNN Architectures (0) | 2021.01.23 |
| EECS 498-007 / 598-005 한국어 강의 (0) | 2021.01.20 |
| EECS 498-007 / 598-005 Assignment #2-2 (1) | 2021.01.16 |
| EECS 498-007 / 598-005 Assignment #2-1 (0) | 2021.01.16 |

